Data structure
- Data Structure is a branch of Computer Science.
- A data structure is a storage that is used to store and organize all the data items.
- used for processing, retrieving, and storing data.
Why do we use data structure
- Necessary for designing efficient algorithms.
- It helps to organization of all data items within the memory.
- It requires less time.
- Easy access to the large database.
Classification/ Types of Data structure
- Linear data structure - allows data elements to be arranged in a sequential or linear fashion.
Example: arrays, linked lists, stack, and queue etc.
- Non-Linear data structure - It is a form of data structure where the data elements do not stay arranged linearly or sequentially.
Example: Tree, graph etc.
Terminologies in Data structure
- Data -- Data are values or set of values.
- Data Item -- Data item refers to single unit of values.
- Entity -- An entity is that which contains certain attributes or properties, which may be assigned values.
- Entity Set -- Entities of similar attributes form an entity set.
- Field -- Field is a single elementary unit of information representing an attribute of an entity.
- Record -- Record is a collection of field values of a given entity.
- File -- File is a collection of records of the entities in a given entity set.
Datatypes in C programming
- Primitive Data Types – It is the most basic data types that are used for representing simple values such as:
-- Integers – 23, 33432 ,342342 etc.
-- Float – 23.2342, 232.00,2342.0000,323.323 etc.
-- Characters - ‘2’, ‘a, ‘$’, ‘@,’g’ etc.
-- Void – used to specify the type of functions which returns nothing.
- Non-Primitive Data Types – It is derived from primitive data types.
-- Arrays
-- Linked-list
-- Queue
-- Stack etc.
Algorithm
- An algorithm is a step-by-step procedure of any problem.
- Criteria of an algorithm --
1. Input
2. Output
3. Definiteness
4. Finiteness
5. Effectiveness
Way of analyzing an algorithm --
1.Best case 2. Average case 3. Worst case
Complexity of an algorithm --
- Complexity in algorithms refers to the amount of resources required to solve a problem or perform a task.
- Resources may be time and space.
Types of Complexities of an algorithm --
- Time complexity of an algorithm is the amount of time it needs to run to completion.
- Space complexity of an algorithm is the amount of space it needs to run to completion.
- order of Complexity of an algorithm --
O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(3^n) < O(n!)
Asymptotic Notation
It is used to write possible running time for an algorithm.It also referred to as 'best case' and 'worst case' scenarios respectively.
- Big-oh notation:
- It is the method of expressing the upper bound of an algorithm's running time.
- It is the measure of the longest amount of time. The function f (n) = O (g (n))
- f(n) <= c.g(n) where n>n0
- Example: 3n+2=O(n) as 3n+2≤4n for all n≥2
- Big-Omega notation:
- It is the method of expressing the lower bound of an algorithm's running time.
- It is the measure of the smallest amount of time. The function f (n) = Ω(g (n))
- f(n) >= c.g(n) where n>n0
- Example: 3n-3= Ω (n) as 3n-3 >=2n for all n≥3
- Theta(Θ) notation:
- It is the method of expressing the both lower and upper bound of an algorithm's running time.
- It is the measure of the average amount of time. The function f (n) = Θ(g (n))
- c1.g(n) <= f(n) <= c2.g(n) where n>n0
- Example: 3n-3=O(n) as 2n<= 3n-3 <= 4n for all n≥3
Time-Space Trade-Off in Algorithms
- It is a problem solving technique in which we solve the problem:
- Either in less time and using more space, or
- In very little space by spending more time.
- The best algorithm is that which helps to solve a problem that requires less space in memory as well as takes less time to generate the output.
- it is not always possible to achieve both of these conditions at the same time.
Abstract Data type (ADT)
- It is a type (or class) for objects whose behaviour is defined by a set of values and a set of operations.
- The definition of ADT only mentions what operations are to be performed but not how these operations will be implemented.
- Example : if we talk about LIST then here we can store multiple value and it has many built in function so that we will work on that data .
Function such as insert(), delete(), pop(), remove() etc.
Array
- An array is a collection of items stored at contiguous memory locations.
- Array is linear data structure. It is one of the simplest DS.
- The idea is to store Multiple items of the same type together.
- Syntax -- type variable_name [size];
- Example – int arr[10]; this is a array declaration of the array now here we can only store 10 integer values in this array
- Array has two type:
1. One dimensional 2. Multidimensional
- One dimensional Array :
- Array represented as one-one dimension such as row or column and that holds finite number of same type of data items is called 1D array .
- Example -- int arr[10];
- Multi-dimensional Array :
- Array represented as more than one dimension . there are no restriction to number of dimensions that we can have.
- Example -- int arr[2][4][5];
Application of Array :
- Arrays can be storing data in tabular format
- It is used to implement vectors, and lists in C++ STL.
- Arrays are used as the base of all sorting algorithms.
- It is used to implement other DS like stack, queue, etc.
- Used for implementing matrices.
- Graphs are also implemented as arrays in the form of an adjacency matrix etc.
Sparse Matrix
- It is matrix in which most of the elements of the matrix have zero value .
- Only we stored non-zero elements with triples- (Row, Column, value).
- Array representation of Sparse Matrix –
Linked list representation of sparse matrix –
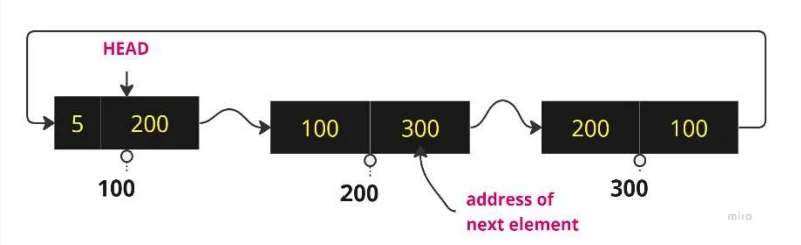
Linked List
- A linked list is a collection of “nodes” connected together via links.
- These nodes consist of the data to be stored and a pointer to the address of the next element .
- Linked list has multiple types:
1. singly linked list 2. Doubly linked list 3. Circular linked list
Singly Linked List (SLL)
- It is a linear data structure in which the elements are not stored in contiguous memory locations .
- Each element is connected only to its next element using address.
Representation Node of SLL :
struct node{
int data; //data item for storing value of the node
struct node *next; //address of the next node
};
Create Node of SLL:
struct Node* Node(int data){
struct Node* newNode=(structNode*)malloc(sizeof(struct Node ));
newNode->data=data;
newNode->next=NULL;
return newNode;
}
Advantage & Disadvantage of singly linked list
Advantages:
- very easier for the accessibility of a node in the forward direction.
- the insertion and deletion of a node are very easy.
- require less memory when compared to doubly, circular linked list.
- very easy data structure
- Insertion and deletion of elements don’t need the movement of all the elements when compared to an array.
Disadvantages :
- Accessing the preceding node of a current node is not possible as there is no backward traversal.
- Accessing of a node is very time-consuming.
Doubly Linked List(DLL)
- A DLL is a complex version of a SLL .
- A DLL has each node pointed to next node as well as previous node.
Representation Node of DLL :
struct node
{
int data; //data item for storing value of the node
struct node *next; //address of the next node
struct node *prev; //address of the previous node
};
Create Node of DLL:
struct Node* Node(int data){
struct Node* newNode=(structNode*)malloc(sizeof(struct Node ));
newNode->prev= NULL;
newNode->data=data;
newNode->next=NULL;
return newNode;
}
Advantage & Disadvantage of DLL
Advantages:
- It is bi-directional traversal
- It is efficient deletion
- Insertion and deletion at both ends in constant time
Disadvantages :
- Increased memory usage
- More complex Implementation
- It is slower traversal
Circular Linked List (CLL)
- All nodes are connected to form a circle.
- the first node and the last node are connected to each other which forms a circle.
- There is no NULL at the end.
Operations on CLL
- Insert at beginning
- Insert at specific Position
- Insert at end
- delete at beginning
- delete at specific position
- delete at end
Advantage & disadvantage of CLL
Advantages:
- No need for a NULL pointer
- Efficient insertion and deletion
- Flexibility
Disadvantages :
- Traversal can be more complex
- Reversing of circular list is a complex as SLL.
Row major order & Column major order
int arr[2][3]=
{ {1,2,3},
{4,5,6} } //2D array
//row major order
{1,2,3,4,5,6}
//column major order
{1,4,2,5,3,6}
Address of any element in 1D array
Address of A[I] = B + W * (I – LB)
I =element, B = Base address, LB = Lower Bound
W = size of element in any array(in byte),
Example: Given the base address of an array A[1300 ………… 1900] as
1020 and the size of each element is 2 bytes in the memory, find the
address of A[1700].
Solution :
Address of A[I] = B + W * (I – LB)
Address of A[1700] = 1020 + 2 * (1700 – 1300)
= 1020 + 2 * (400) = 1020 + 800=1820
Address of any element in 2D array
Row major order : A[I][J] = B + W * ((I – LR) * N + (J – LC))
I = Row element , j=column element , LR=lower limit of row
N = No. of column given in the matrix , LC=lower limit of column
Example: Given an array, arr[1………10][1…….15] with base value 100 and the size of each element is 1 Byte in memory. Find the address of arr[8][6] with the help of row-major order.
Formula:
Address of A[I][J] = B + W * ((I – LR) * N + (J – LC))
Solution:
N = Upper Bound column – Lower Bound column + 1
A[8][6] = 100 + 1 * ((8 – 1) * 15 + (6 – 1)) = 100 + 1 * ((7) * 15 + (5))
= 100 + 1 * (110)=210
Column major order :
A[I][J] = B + W * ((J– LC) * M + (I – LR))
N = No. of rows given in the matrix
Example: Given an array, arr[1………10][1………15] with base value 100 and the size of each element is 1 Byte in memory. Find the address of arr[8][6] with the help of row-major order.
Formula:
A[I][J] = B + W * ((J– LC) * M + (I – LR))
Solution:
M = Upper Bound row – Lower Bound row + 1
A[I][J] = B + W * ((J – LC) * M + (I – LR))
A[8][6] = 100 + 1 * ((6 – 1) * 10 + (8 – 1))
= 100 + 1 * ((5) * 10 + (7))= 100 + 1 * (57)= 157


.png)












very nice lekin yr thora or explain karo isko itne short point me aktu me marks nh milega
ReplyDelete