Unit 3 | DSTL Notes |Discrete Structure and Theory of Logic Notes | Aktu Notes

Unit 3 | DSTL Notes |Discrete Structure and Theory of Logic Notes | Aktu Notes

Proposition

- "Proposition" typically refers to a declarative statement

- that can either be true or false, but not both.

- Propositions are fundamental to logic and form the basis of reasoning and proofs in mathematics.

- They are often represented symbolically (p,q,r etc) and manipulated using logical operators such as AND, OR, NOT, IMPLIES, etc.

- Example:

   -  "2 + 2 = 4" is a proposition, and it is true. 

   -  "5 is a prime number" is a proposition, and it is true. 

   -  "The moon is made of cheese" is a proposition, and it is false.

Compound Proposition

- A compound proposition is formed by composition

- of two or more propositions called components or sub-propositions.

- For example 

   -  Risabh is intelligent and he studies hard. 

   -  Sky is blue and clouds are white.

Connectives

- Connectives are symbols or words used to combine or modify propositions.

 

Examples of connectives:

- "It is raining AND it is windy."

- I will have pizza OR I will have pasta for dinner."

- "It is NOT raining."

- "If it is raining, THEN I will take an umbrella."

- I will go to the party IF AND ONLY IF my friends are going

Conjunction (AND)

Denoted by ∧, it represents the logical "and" operation. For example, "p ∧ q" means "p and q".

Disjunction (OR)

Denoted by ∨, it represents the logical "or" operation. For example, "p ∨ q" means "p or q".

Negation (NOT)

Denoted by ¬ or ~, it represents the logical "not" operation. For example, "¬p" means "not p".

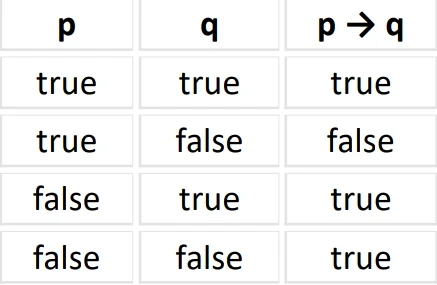
Implication (IMPLIES)

Denoted by → or ⇒, it represents the logical "implies" operation. For example, "p → q" means "if p, then q".

Biconditional (IF AND ONLY IF)

Denoted by ↔ or ⇔, it represents the logical "if and only if" operation. For example, "p ↔q" means "p if and only if q".

Converse

- The converse of a conditional statement P→Q is Q→P.

- Example: If it's raining, then I'll bring an umbrella.

- Converse: If I'm bringing an umbrella, then it's raining.

Contrapositive

- The contrapositive of a conditional statement P→Q is ¬Q→¬P.

- Contrapositive: If I'm not bringing an umbrella, then it's not raining.

Inverse

- The inverse of a conditional statement P→Q is ¬P→¬Q.

- Inverse: If it's not raining, then I won't bring an umbrella.

Well Formed Formula

- It is typically constructed from propositional variables ( atomic formulas) and logical connectives.

- The rules for constructing.

- well-formed formulas are used to represent logical statements or propositions.

 

1. An atomic statement P is considered a well-formed formula.

2. If P is a well-formed formula, then ¬P (negation) is also a well- formed formula.

3. If P and Q are well-formed formulas, then (P∨Q), (P∧Q), (P→Q), and (P↔Q) are also well-formed formulas.

4. A statement composed of variables, parentheses, and connectives is recursively a well-formed formula if it can be derived by applying the above rules.

Examples of WFF

1. ¬(P∧Q)∨ R (false) --> (¬(P∧Q))∨ R or ¬((P∧Q)∨ R)

2. (P∧Q) , ((P∨ Q)∧(¬P∨ R)) , (¬(P→Q)∨ R) (true)

Logical Equivalence

- If two propositions P and Q where p, q, ..... are propositional variables, have the same truth values

- in every possible case, the propositions are called logically equivalent or simply equivalent, and denoted by P ≡ Q

1. ¬(P→Q)≡P∧¬Q

2. P→Q≡¬P∨Q

3. P↔Q≡(P→Q)∧(Q→P)

4. ¬(P↔Q)≡(P∧¬Q)∨(¬P∧Q)

5. P↔Q)∨(Q↔R)≡P↔R

Tautology

- A tautology is a statement that is always true, regardless of the truth values of its variables.

- Example: P∨¬P ( "Either it's raining or it's not raining.")

Contradiction

- A contradiction is a statement that is always false, regardless of the truth values of its variables.

- Example: P∧¬P ("It's both raining and not raining.")

Contingency

- A statement is contingent if it is neither a tautology nor a contradiction, meaning it can be true or false depending on the truth values of its variables.

- Example: P→Q ("If it's raining, then it's cloudy.")

Satisfiability

- A statement is satisfiable if there exists at least one assignment of truth values to its variables that makes the statement true.

- Example: P∨Q ("It's raining and it's sunny.")

Laws of Proposition

Question:

Prove (p → q) ∧ (p → r) ≡ p →(q ∧ r).

≡ (¬ p ∨ q) ∧ (¬ p ∨ r) Substitution for →, twice

≡ ¬p ∨ (q ∧ r) Distribution law

≡ p → (q ∧ r) Substitution for →

Valid Argument

- The proof is a valid argument that determines the truth values of mathematical statements.

- The argument is a set of statements or propositions

Example 1:

Premise: Every mother is a woman.

Premise: All women are caring.

Conclusion: Therefore, every mother is caring.

Example 2: 

Premise: All humans have wings.

Premise: Birds have wings.

Conclusion: Therefore, all humans are birds.

Rules of Inference

- Rules of inference are logical principles or techniques

- used to justify the validity of logical arguments or deductions.

- They provide a systematic way to derive new conclusions from given premises.

- Here are some common rules of inference:

- Premises are statements or propositions that are assumed to be true in an argument or logical deduction

Numerical: For students to do well in discrete structure course, it is necessary

that they study hard. Students who do well in courses do not skip classes. Student who study hard do well in courses. Therefore students who do well in discrete structure course do not skip class.

Given the propositional variables:

p→"Do well in the course.

q→"They study hard.

r→"Do not skip classes.

1. For students to do well in the discrete structure course, it is necessary that they study hard: p→q

2. Students who do well in the courses do not skip classes: p→r

3. Students who study hard do well in courses: q→p

4. Therefore, students who do well in the discrete structure course do not skip classes: p→r

Given premises: i) p→q ii) p→r iii) q→p Conclusion: p→r

Proof:

Step1: 

Taking premise III (q → p) and premise II (p → r) together: 

q→p and p→r give q→r (Using hypothetical syllogism).

Step2: 

Now, taking premise I (p → q) and the result from step 1:

p→q and q→r give p→r (Using hypothetical syllogism).

Therefore, the conclusion p→r is valid.

First-order Logic

- First-order logic extends propositional logic by quantifying and generalizing over a given universe.

- Also known as first-order predicate calculus, attributing properties to individual entities.

- Predicate calculus: A generalized form of propositional calculus for manipulating statements.

- Universe of Discourse (UD): Set encompassing all potential values for predicate variables.

Quantifiers

- Universal Quantifier: Symbolized by ∀ , signifies "for all" or "for every" element in a set.

- Existential Quantifier: Symbolized by ∃ , denotes "for some" or "there exists" elements in a set.

Rules of Inference

i) Universal specification: By this rule if the premise (∀x) P(x) is true then P(c) is true where c is particular member of UD.

(∀x)P(x)

-------------

 ∴ P(c)

ii) Universal generalization: By this rule if P(c) is true for all e in UD then (∀x) P(x) is true.

  P(c)

----------------

∴ (∀x)P(x)

x is not free in any of given premises.

iii) Existential specification: By this rule if (∃x) P(x) is true then P(x) is true for some particular member of UD.

(∃x)P(x)

-------------

 ∴ P(c)

c is some member of UD.

iv) Existential generalization: By this rule if P(c) is true for some particular member c in UD, then (∃x) P(x) is true

  P(c)

---------------

∴ (∃x)P(x)

c is some member of UD.